TL Catenary
Win32 and 64, EnglishGeneral Usage Instructions
Click on any of the app icons installed in the Add-ins tab (or run the commands directly by typing them in the command area in AutoCAD) and follow the onscreen prompts to select the input parameters and generate a catenary polyline. All catenary commands operate within the current UCS XY plane. The program supports custom user coordinate systems (UCS). If any other orientation is desired adjust the UCS accordingly prior to running any of the catenary commands.
Below is a list of all Catenary commands and their input parameters:
TLCatenaryA
Generates a catenary curve using a base point and a parameter "a" specified by the user
Inputs:
* Non-zero value for the parameter "a". A positive value will result in a "hanging" curve in the direction of gravity, whereas a negative value will result in a "standing" curve in the opposite direction of gravity. The gravity vector is defined as (0,-1) based on the current UCS.
* Left distance - how far to the left of origin to draw the catenary curve. Used internally to compute the location of the First Point. Value must be positive
* Right distance - how far to the right of origin to draw the catenary curve. Used internally to compute the location of the Second Point. Value must be positive
* Origin point - the location of the "origin" or (0,0) of the Catenary curve. The general equation of the Catenary curve is y[x] = a * Cosh((x-h)/a) + v, where a is the parameter a, h is the horizontal offset and v is the vertical offset. The origin point therefore has coordinates (h,v)
Potential issues: Evaluation of the catenary equation at the polyline points may result in numerical overflow in which cases the point will be excluded from the final polyline
TLCatenaryLength
Generates a catenary curve using a start and end points and a total length specified by the user
Inputs:
* A non-zero length of the catenary curve. A positive value will result in a "hanging" curve in the direction of gravity, whereas a negative value will result in a "standing" curve in the opposite direction of gravity. The gravity vector is defined as (0,-1) based on the current UCS.
* First point - location of the first anchor point of curve.
* Second point - location of the second anchor point of curve.
Potential issues: The distance between the input points must be less than the length of the curve. Additionally the points may not coincide or be vertically aligned in the direction of gravity.
TLCatenarySlope
Generates a catenary curve using a start and end points and a slope at a location all specified by the user
Inputs:
* A value for the slope of the catenary curve. The first derivative of the catenary curve is the slope of the tangent at a specified point. Values may be negative (catenary curve is decreasing or sloping down), zero (sag/crest point) or positive (curve is sloping up or increasing). Refer to the diagram for a visual representation of the definition.
* Slope location point - used to determine the location along the horizontal axis (x) of the curve where the slope value is to be applied.
* First point - location of the first anchor point of curve.
* Second point - location of the second anchor point of curve.
Potential issues: Large positive/negative values for the slope will result in extreme catenary geometry causing numerical overflows. Additionally the points may not coincide or be vertically aligned in the direction of gravity.
TLCatenarySag
Generates a catenary curve using a start and end points and a sag specified by the user
Inputs:
* A value for the sag of the catenary curve. A positive value will result in a "hanging" curve in the direction of gravity, whereas a negative value will result in a "standing" curve in the opposite direction of gravity. A value of zero will effectivly generate a half-curve. Refer to the diagram for a visual representation of the definition.
* First point - location of the first anchor point of curve.
* Second point - location of the second anchor point of curve.
Potential issues: Large positive/negative values for the sag will result in extreme catenary geometry causing numerical overflows. Additionally the points may not coincide or be vertically aligned in the direction of gravity.
TLCatenaryBulge
Generates a catenary curve using a start and end points and a bulge specified by the user
Inputs:
* A non-zero value for the bulge of the catenary curve. A positive value will result in a "hanging" curve in the direction of gravity, whereas a negative value will result in a "standing" curve in the opposite direction of gravity. The catenary bulge is defined as the max distance between the catenary points perpendicular to the line defined by the control points. Refer to the diagram for a visual representation of the definition.
* First point - location of the first anchor point of curve.
* Second point - location of the second anchor point of curve.
Potential issues: Control points may not coincide or be vertically aligned in the direction of gravity.
TLCatenaryVerticalBulge
Generates a catenary curve using a start and end points and a vertical bulge specified by the user
Inputs:
* A non-zero value for the vertical bulge of the catenary curve. A positive value will result in a "hanging" curve in the direction of gravity, whereas a negative value will result in a "standing" curve in the opposite direction of gravity. The catenary vertical bulge is defined as the max distance (or vertical clearance) between the catenary points taken along the y axis to the line defined by the control points. Refer to the diagram for a visual representation of the definition.
* First point - location of the first anchor point of curve.
* Second point - location of the second anchor point of curve.
Potential issues: The solution function of this type of catenary equations exhibit chaotic behaviour with potentially infinite number of solutions. The app solver will impose additional restriction on the solution domain by rejecting all solutions with a vertical bulge location falling outside the line between the two control points. Additionally the control points may not coincide or be vertically aligned in the direction of gravity.
TLCatenaryArea
Generates a catenary curve using a start and end points and enclosed area specified by the user
Inputs:
* A non-zero value for the area of the catenary curve. A positive value will result in a "hanging" curve in the direction of gravity, whereas a negative value will result in a "standing" curve in the opposite direction of gravity. The catenary area is defined as the area enclosed by the catenary curve and the line connecting the two control points. Refer to the diagram for a visual representation of the definition.
* First point - location of the first anchor point of curve.
* Second point - location of the second anchor point of curve.
Potential issues: The control points may not coincide or be vertically aligned in the direction of gravity.
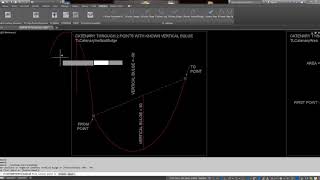
TLCatenaryPoints
Generates a catenary curve trough three known points specified by the user
Inputs:
* First point - location of the first anchor point of curve.
* Second point - location of the second anchor point of curve.
* Third point - location of the last anchor point of curve.
Potential issues: All three points must be unique. No pair of points may be vertically aligned in the direction of gravity and finally the points may not be collinear
TLCatenaryBestFit
Generates a catenary curve by performing a least squares error function optimization on a set of input points.
The Error function is defined as the sum of squares of the catenary residuals at every point in the set.
In addition to the standard output a residuals list is generated for all input points along with the final value of the error function.
Inputs:
* A set of control points which are all presumed to lie on the same catenary curve. Points may be auto-extracted from existing acad polyline or manually input from the command line
Potential issues: Number of control points n must be more than two. If n is three the result will be identical to the three-point catenary. For values of n > 3 a least squares optimization will be performed. This is a relatevly CPU intensive operation. Due to the highly non-linear nature of the catenary equations potentially infinite number of local solutions exist. The app solver will impose additional restrictions on the solution domain by rejecting solutions which deviate too far from the parameters of a three point catenary curve computed from the first, middle and last point of the input set (pre-sorted along the X direction). Such solution may not exist for widely spread apart input points. In all cases for best results as a general recommendation try to eliminate all outliers from the input set beforehand.
Commands
| Ribbon/Toolbar Icon | Command | Command Description |
|---|---|---|

|
TLCatenaryA |
Generates a catenary curve using a base point and a parameter "a" specified by the user |

|
TLCatenaryA3d |
Launches the TLCatenaryA command in 3D mode. This mode changes the coordinate system internally so that the vector of gravity is aligned with the Z axis of the current/active UCS and the Catenary XY plane is aligned with the two control points. All coordinates are still transformed back to the current UCS, but the Catenary equation parameters are reported in the internal coordinate system |

|
TLCatenaryLength |
Generates a catenary curve using a start and end points and a total length specified by the user |

|
TLCatenarySlope |
Generates a catenary curve using a start and end points and a slope at a location all specified by the user |

|
TLCatenarySag |
Generates a catenary curve using a start and end points and a sag specified by the user |

|
TLCatenaryBulge |
Generates a catenary curve using a start and end points and a bulge specified by the user |

|
TLCatenaryVerticalBulge |
Generates a catenary curve using a start and end points and a vertical bulge specified by the user |

|
TLCatenaryArea |
Generates a catenary curve using a start and end points and enclosed area specified by the user |

|
TLCatenaryPoints |
Generates a catenary curve trough three known points specified by the user |

|
TLCatenaryBestFit |
Generates a catenary curve by performing a least squares error function optimization on a set of input points. The Error function is defined as the sum of squares of the catenary residuals at every point in the set. In addition to the standard output a residuals list is generated for all input points along with the final value of the error function. |

|
TLCatenaryActivate |
Activates the TL Catenary App with the Autodesk App Store. Active internet connection is required. Once activated the app can be used offline. This command is not available in the ribbon and needs to be manually typed in at the AutoCAD command prompt |
Installation/Uninstallation
The installer that ran when you downloaded this app/plug-in from Autodesk App Store will start installing the app/plug-in. OR, simply double-click the downloaded installer to install the app/plugin. You may need to restart the Autodesk product to activate the app/plug-in. To uninstall this plug-in, exit the Autodesk product if you are currently running it, simply rerun the installer, and select the "Uninstall" button. OR, click Control Panel > Programs > Programs and Features (Windows 7/8.1/10/11) and uninstall as you would any other application from your system.
Once the installation is complete, start AutoCAD and login with your Autodesk user id and password. Run the TLCatenaryActivate command to activate the app. Once activated the app can be used offline.
Additional Information
Known Issues
In certain special cases the catenary curve is undefined: for example when all three points lie on the same line or where vertical points exist etc. Additionally certain input parameters may cause the catenary to shoot off to positive/negative infinity quite rapidly. In those extreme cases due to reasons such as limitations of the computer floating point numbers range, numerical instability, round-off errors etc the program might not be able to compute all catenary points. No polyline or incomplete polyline may be generated.
Contact
Author/Company Information
Support Information
For questions/comments/suggestions/bug reports etc please send an email to Todor.Latev@gmail.com.
Version History
| Version Number | Version Description |
|---|---|
|
2023.6.3.1 |
TLCatenaryBestFit command updated to allow selection of multiple Autocad point objects |
|
2019.9.10.1 |
Added 2024 support |
|
2018.12.28.1 |
Added 2020 support |
|
2018.10.10.1 |
Initial release |